- What is the Law of Universal Gravitation?
- Statement of the Law of Universal Gravitation
- Formula of the Law of Universal Gravitation
- Examples of the Law of Universal Gravitation
We explain what the Law of Universal Gravitation is, what its formula and its statement are like. Also, examples of the use of your formula.
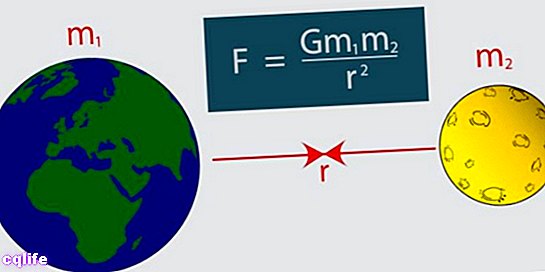
What is the Law of Universal Gravitation?
The Law of Universal Gravitation is one of the lawsphysical formulated by Isaac Newton in his bookPhilosophiae Naturalis Principia Mathematicaof 1687. It describes the gravitational interaction between massive bodies, and establishes a relation of proportionality of the Gravitational force with the mass of the bodies.
To formulate this law, Newton deduced that the force with which two masses attract each other is proportional to the product of their masses divided by the distance that separates them squared. These deductions are the result of empirical verification by means of the observation.
The law implies that the closer and more massive two bodies are, the more intensely they will attract each other. Like other Newtonian laws, it represented a leap forward in the scientific knowledge of the time.
However, today we know that, from a certain amount of mass, this law loses its validity (in the case of supermassive objects), and it is necessary to work with the Law of General Relativity formulated in 1915 by Albert Einstein. The Law of Universal Gravitation is then an approximation to Einstein's law but it is still useful to understand most of the gravitational phenomena of the world.Solar system.
Statement of the Law of Universal Gravitation
The formal statement of this Newtonian law holds that:
"The force with which two objects attract is proportional to the product of their masses and inversely proportional to the square of the distance that separates them."
This means that any two bodies attract each other with a greater or lesser force depending on their mass is greater or less, and according to the distance between them.
Formula of the Law of Universal Gravitation
The fundamental formula of the Law of Universal Gravitation is as follows:
F = | (G. M1. M2) / r² | . r *
Where:
- F is the force of attraction between two masses
- G is the universal constant of gravitation (6.673484.10-11 N.m2 / kg2)
- m1 is the mass of one of the bodies
- m2 is the mass of another of the bodies
- r the distance that separates them.
- r * is the unit vector that indicates the direction of the force.
If the attractive forces of each body are calculated (the force that mass 1 makes on 2 and vice versa), we will have two forces equal in module and of opposite direction. To obtain this difference in signs, it is necessary to write the equation as follows:
F12 = | G. m1.m2 / (r11-r2) 3 | . (r1-r2)
Where changing 1 by 2 we obtain the force for each case. Written this way, the vector (r1-r2) gives the correct direction (the sign) for each force.
Examples of the Law of Universal Gravitation
Let's solve a couple of exercises as an example of the application of this formula.
- Suppose that an 800-kg mass and a 500-kg mass attract each other in a vacuum, separated by a space of 3 meters. How can we calculate the force of attraction they experience?
Simply applying the formula:
F = G. (m1.m2) / r2
Which will be: F = (6.67 × 10-11 N.m2 / kg2). (800 kg. 500 kg) / (3m) 2
And then: F = 2,964 x 10-6 N.
- Another exercise: At what distance must we place two bodies of mass of 1 kg, so that they attract with a force of 1 N?
Starting from the same formula
F = G. (m1.m2) / r2
We will clear the distance, staying that r2 = G. (m1.m2) / F
Or what is the same: r = √ (G. [m1.m2]) / F
That is: r = √ (6.67 × 10-11 N.m2 / kg2. 1kg x 1kg) / 1N
The result is that r = 8.16 x 10-6 meters.
