triangle

Mathematics

2022

We explain everything about the triangle, its properties, elements and classification. Also, how its area and perimeter are calculated.

Triangles are flat, basic geometric figures.

What is a triangle?

The triangles or trines are geometric figures flat, basic, that have three sides in contact with each other at common points called vertices. Its name comes from the fact that it has three interior or internal angles, formed by each pair of lines in contact at the same vertex.

These geometric figures are named and classified according to the shape of their sides and the type of angle they make. However, its sides are always three and the sum of all its angles will always give 180 °.

Triangles have been studied by the humanity since time immemorial, since they have been associated with the divine, with mysteries and magic. Therefore, it is possible to find them in many occult symbols (masonry, witchcraft, kabbalah, etc.) and in traditions religious. Its associated number, three, numerologically alludes to the mystery of conception and life itself.

In the history of the triangle the greek antiquity deserves a prominent place. The Greek Pythagoras (c. 569 - c. 475 BC) proposed his famous theorem for right triangles, which states that the square of the hypotenuse is equal to the sum of the square of the legs.

Triangle properties

The most obvious property of triangles are their three sides, three vertices, and three angles, which may well be similar or totally different from each other. Triangles are the simplest polygons there are and they lack a diagonal, since with any three non-aligned points it is possible to form a triangle.

In fact, any other polygon can be divided into an ordered set of triangles, in what is known as triangulation, so the study of triangles is fundamental to geometry.

Also, triangles are always convex, never concave, since their angles can never exceed 180 ° (or π radians).

Triangle elements

Triangles are made up of three sides that meet at three vertices.

Triangles are made up of several elements, many of which we have already mentioned:

  • Vertices. These are the points that define a triangle by joining two of them with a straight line. Thus, if we have points A, B and C, joining them with lines AB, BC and CA will give us a triangle as a result. Also, the vertices are on the opposite side of the interior angles of the polygon.
  • Sides. This is the name given to each of the lines that join the vertices of a triangle, delimiting the figure (the inside from the outside).
  • Angles. Every two sides of a triangle form at their common vertex some type of angle, which is called an interior angle, since it faces the inside of the polygon. These angles are, like the sides and vertices, always three.

Triangle types

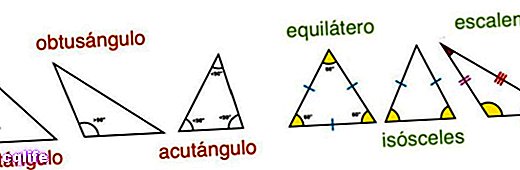
Triangles can be classified according to their angles or according to their sides.

There are two main classifications of triangles:

  • According to its sides. Depending on the relationship between its three different sides, a triangle can be:
    • Equilateral. When all three sides have the exact same length.
    • Isosceles. When two of its sides have the same length and the third a different one.
    • Scalene. When its three sides have different lengths from each other.
  • According to their angles. Depending instead on the opening of its angles, we can speak of triangles:
    • Rectangles. They present a right angle (90 °) made up of two similar sides (legs) and opposite to the third (hypotenuse).
    • Oblique angles Those that do not present any right angle, and that in turn can be:
      • Blunt angles. When any of its interior angles is obtuse (greater than 90 °) and the other two acute (less than 90 °).
      • Acute angles. When its three interior angles are acute (less than 90 °).

These two classifications can be combined, allowing us to speak of isosceles right triangles, scalene acute triangles, etc.

Perimeter of a triangle

The perimeter of a triangle is calculated by adding its sides.

The perimeter of a triangle is the sum of the lengths of its sides, and is usually denoted by the letter p or with 2s. The equation to determine the perimeter of a given triangle ABC is:

p = AB + BC + CA.

For example: a triangle whose sides are 5cm, 5cm and 10cm will have a perimeter of 20cm.

Area of ​​a triangle

To calculate the area of ​​the triangle it is necessary to know its height.

The area of ​​a triangle (a) is the interior space delimited by its three sides. It can be calculated knowing its base (b) and its height (h), according to the formula:

a = (b.h) ​​/ 2.

Area is measured in units of length squared (cm2, m2, km2, etc.)

The base of a triangle is the side on which the figure "rests", usually the bottom. Instead, to find the height of a triangle, we need to draw a line from the vertex opposite the base, that is, the top angle. That line should form a right angle with the base.

Thus, for example, having an isosceles triangle with sides: 11 cm, 11 cm and 7.5 cm, we can calculate its height (7 cm) and then apply the formula: a = (11 cm x 7 cm) / 2, which yields a result of 38.5 cm2.

Other geometric figures

The square, the rectangle, and the circle are the other simple geometric figures.

Other two-dimensional geometric figures of importance are:

  • The square. Polygons with four perfectly equal sides, two-dimensional ancestors of the cube.
  • The rectangle. If we take a square and lengthen two of its opposite sides, we will obtain a figure composed of four lines: two equal and two different (but equal to each other). That is a rectangle.
  • The circle. We all know the circle, one of the simplest forms of geometry and which consists of a continuous curved line that returns to the starting point tracing 360 ° of circumference.
!-- GDPR -->